Volver a la página Analizador de Sudoku principal.
Lo que sigue asume que usted ya está familiarizado con la Cuadrícula de eliminación de CyberJerry y los basicos de escribir con lápiz todos los candidatos posibles para cada celda sin resolver. Aún más que las otras técnicas avanzadas, el método de MutEx exige que usted sea muy meticuloso y esmerado en cada paso.
Para emplear en papel la técnica MutEx, usted va a construir cadenas de 2 colores de pares mutuamente exclusivos. Va a destacar los candidatos numéricos con marcadores transparentes de colores contrastantes, o encerarlos con crayones o lápices de color. Se recomiendan marcadores o lápices borrables. Tal vez se necesitarán más colores para construir cadenas secundarias tentativas.
Empezamos por reconocer dos situaciones en que dos candidatos son mutuamente exclusivos. En ambos casos, un número debe ser correcto, y el otro falso. Podemos destacar los dos candidatos con colores contrastantes para ilustrar esta relación mutuamente exclusiva:
| A. Una celda sin resolver con exactamente dos candidatos posibles. | 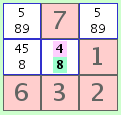 ejemplo A |
B. Un número que se encuentra exactamente dos veces en una fila, columna, o un cuadrado 3x3. | 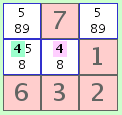 ejemplo B |
 fig. 1a |
 fig. 1b |
Ahora note que podemos enlazar juntos A con B, como ilustrado en figura 1a. Mire el '4' en la celda izquierda y el '8' en la central. Desde ambos son enlazados al '4' en la celda central en relaciones mutuamente exclusivas, ambos deben tener el mismo color. Porque si el rosado '4' es correcto, ambos el verde '4' y el verde '8' deben ser falsos. Si el rosado '4' es falso, ambos números verdes deben ser correctos. Es decir que si el '4' en la celda izquierda es correcto, el '8' en la central también debe ser correcto. También si uno es falso, ambos deben ser falsos. Y, porque se pueden intercambiar los dos colores, fig. 1b igualmente demuestra las relaciones mutuamente exclusivas entre los candidatos.
El texto de ayuda en la area de 'Mensajes' de CyberJerry puede describir la cadena arriba así:
8@h2 -> 4@h2 -> 4@h1que es una manera abreviada de decir, "El '8' en celda h2 tiene una relación mutuamente exclusiva con el '4' en celda h2, lo cual tiene una relación mutuamente exclusiva con el '4' en celda h1".
O, puede decir:
4@h2 -> 8@h2, 4@h2 -> 4@h1que es, "El '4' en celda h2 tiene una relación mutuamente exclusiva con el '8' en celda h2. El '4' en celda h2 también tiene una relación mutuamente exclusiva con el '4' en celda h1".
[Nota 2] Conflictos internos:

fig. 2
8@f3 -> 4@f3 -> 4@f1 -> 4@h1 -> 8@h1 -> 8@h2 -> 4@h2 -> 4@c2 -> 1@c2 -> 1@a1 -> 8@a1que indica que, empezando con el '8' en celda f3, podemos enlazar al '4' en f3 (según ejemplo A arriba), entonces al '4' en celda f1 (según ejemplo B), entonces a los candidatos siguientes, alternando colores hasta el rosado '8' en celda a1. En este punto tenemos el conflicto siguiente:
Se aplica la lógica siguiente:
- Desde los dos colores se representan dos posibilidades mutuamente exclusivas, todos los 6 candidatos rosados deben ser correctos o todos falsos. (La cadena)
- Los dos rosados '8's no pueden ser ambos correctos porque estan en la misma columna. (El conflicto)
- Por lo tanto, los dos rosados '8's deben ser falsos.
- Desde la cadena se representa dos posibilidades mutuamente exclusivas, los 6 candidatos rosados deben ser falsos.
- De más importancia, los 5 candidatos verdes deben ser correctos.

fig. 2a
1@f1 -> 1@d2 -> 8@d2 -> 8@h2 -> 4@h2 -> 4@h1 -> 8@h1, 4@h1 -> 4@f1que produce el conflicto siguiente:
Este conflicto está on poco más obvio que él de fig. 2, mas por fin produce el mismo resultado.
[Nota 3] Conflictos externos:
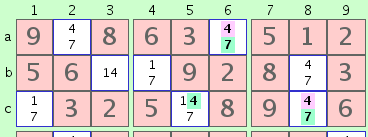
fig. 3
Aúnque esta cadena corta no contiene conflictos internos, produce el siguiente:
Por nuestro sistema de 2 colores, es fácil ver que los dos '7's verdes deben ser ambos correctos o ambos falsos. No pueden ser correctos, porque ese haría no solucionable el cuadrado 3x3 superior izquierdo. Por lo tanto, los 2 candidatos rosados deben ser correctos, así que hemos solucionado dos celdas por sólo un golpe.
[3a]
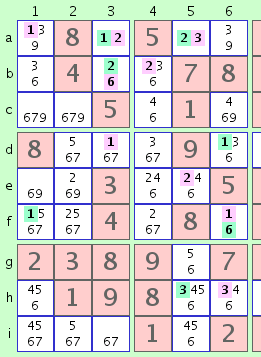
fig. 3a
Si fueron correctos los candidatos verdes, la celda d6 sería un '1'. Si fueron correctos los rosados, la celda h6 sería un '3'. En cualquier caso, la celda d6 no podría ser un '3'.
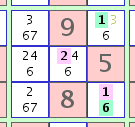
fig. 3b
Sólo un lugar para un '3' en el cuadrado 3x3 central.es decir, hemos solucionado la celda d4. Es un '3'.
[Nota 3c] Extendiendo la cadena:
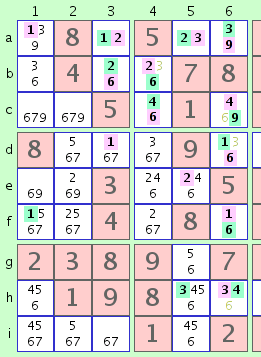
fig. 3c
Ya tenemos en columna 6 un '6' verde y un '6' rosado. Utilizar la misma lógica de arriba, podemos eliminar los otro dos '6's en columna 6 - ellos en celdas c6 y h6. Y por eso podemos extender la cadena como siguiente:
3@h6 -> 4@h6 -> 4@c6 -> 9@c6 -> 9@a6 -> 3@a6, 4@c6 -> 4@c4 -> 6@c4 -> 6@b4Esta cadena extendida, ilustrada en: fig. 3c., ya nos permite eliminar el '3' en celda b4, y quizás otras eliminaciones y/o extensiones.
[Nota 4] Comparar 2 cadenas:

fig. 4
(A propósito, note también que, antes de formar el enlace 3@h4 -> 3@h6 en esta cadena, en primer lugar tuvimos que haber eliminado el '3' en celda h1 por medio de la técnica 'Caja/Línea'.)
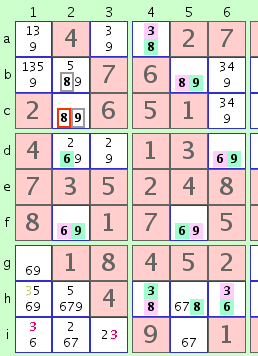
fig. 4a
Éste nos da una situación interesante. Ambas cadenas son completas y no contienen conflictos individualmente, pero juntas producen el conflicto siguiente:
Note dos conflictos entre candidatos de las dos cadenas: El '8' en celda b5 (cadena 1) y el '8' en b2 (cadena 2) no pueden ser ambos correctos. Tampoco el '9' en f2 (cadena 1) y el '9' en c2 (cadena 2). El conflicto inter-cadena es así: desde los dos candidatos en la primera cadena son mutuamente exclusivos, uno debe ser correcto. Pero los dos candidatos en la segunda cadena deben ser de la misma veracidad; o los dos son correctos o los dos son falsos. La única vía que uno de los números mutuamente exclusivos de la primera cadena puede ser correcto es que sean falsos los dos números de color gris en la segunda cadena. Desde los números de color gris son falsos, el rojo (el '8' en celda c2) debe ser correcto, y hemos solucionado esa celda.
Como ya se notó arriba, la técnica MutEx exige bastante paciencia y esmero. Tal vez usted tendría que construir varias cadenas antes de encontrar una cadena o par de cadenas con un conflicto que le permitirá resolver ni siquiera una celda. Pero muchas veces su paciencia puede resultar en varias celdas resueltas por sólo un golpe. Así que, aunque no puedo garantizar que el método MutEx va a resolver todos los Sudokus con exito infalible, yo puedo decir que parece el método del recurso último, habilitando una solución paso a paso para unos Sudokus bastante difíciles, cuando fallan otros métodos.
Ya sé bien que unos expertos de Sudoku ya usan varias versiones de la estratégia de dos colores de pares mutuamente exclusivos. Pues, bien. Creo que mi método de 'MutEx' incluye todas de estas técnicas de 2 colores en una estratégia amplia. Si tiene otra opinión, favor de informarme. También me gusta recibir consejos y preguntas generales. Usted puede utilizar la página de Contacto de este sitio para ver varias formas de comunicarse conmigo.